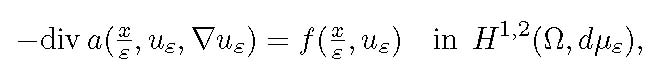
Philip Heuser
Homogenization of multidimentional
structures
We consider multidimensional periodic structures, which can be identified with a periodic positive measure μ on Rn. Using the concept of tangential calculus with respect to measures and related Sobolev spaces H1,p(Ω,dμ), we study the homogenization of nonlinear elliptic equations