Weiterbildungsveranstaltung
Die Mathematik hinter Spielen und Rätseln
|
Die Deutschschweizerische Mathematik-Kommission
und die ETH Zürich
laden Sie herzlich zu dieser Weiterbildungsveranstaltung ein. |

 |
KursdatenOrt: ETH Zürich, Raum HG G19.1 Datum: Dienstag, 25. November 2025, 09:30 Uhr - 16:00 Uhr Organisation: Jonas Gloor (DMK), Norbert Hungerbühler (ETH) Kursbeitrag: |
|

|
Referentin
Dr. Érika Roldán (Max-Planck-Institut für Mathematik in den Naturwissenschaften, und ScaDS.AI Universität Leipzig)
Zielpublikum
Mathematik-Lehrkräfte der Sekundarstufe II
Inhalt
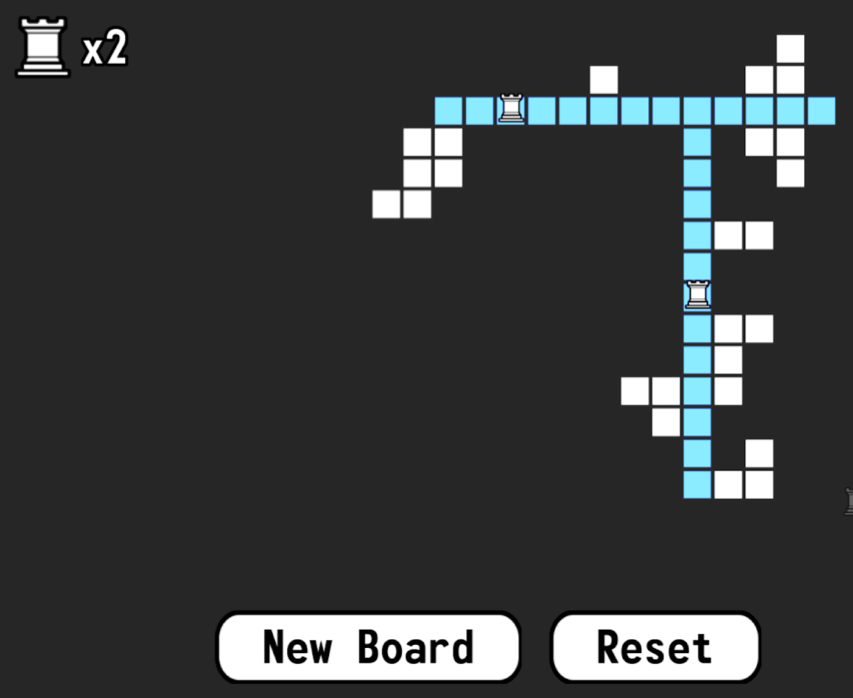
Wie viele Türme oder Damen braucht man, um eine bestimmte
Teilmenge der Felder eines Schachbretts zu „bewachen“? Diese Frage
führt zu einem spannenden mathematischen Problem, das Elemente aus der
Kombinatorik und der Informatik vereint – und direkt mit den Zugregeln
des Schachspiels zusammenhängt.
Diese verallgemeinerten Schachbretter werden Polyominos genannt
– sie müssen turmweise zusammenhängend (rookwise-connected) sein – und
die zentrale Frage lautet: Wie kann man sie mit möglichst wenigen
Schachfiguren vollständig abdecken? Wir werden sehen, warum
höchstens n/2 Türme oder n/3 Damen ausreichen, um ein Polyomino
mit n Feldern zu bewachen – und warum dies in vielen Fällen sogar
notwendig ist. Außerdem werden wir sehen, warum es mathematisch
schwierig (NP-vollständig) ist, die genaue Mindestanzahl der
benötigten Figuren zu bestimmen. Abschließend zeigen wir, wie Sätze
aus der Theorie bipartiter Matchings helfen können, Mengen nicht
schlagender Türme auf Polyominos zu beschreiben.
Neben diesen theoretischen Einsichten stellt der Workshop auch
didaktische Ideen vor, wie dieses Thema gewinnbringend im Unterricht
eingesetzt werden kann – zum Beispiel zur Veranschaulichung von
Optimierungsproblemen, Graphentheorie, algorithmischer Komplexität und
mehr. Dies geschieht anhand von low-floor, no-ceiling-Aufgaben, die
einen niedrigschwelligen Einstieg ermöglichen, aber unbegrenzte
Möglichkeiten zur weiteren Exploration bieten.
Durch die Auseinandersetzung mit aktueller Forschung und offenen
mathematischen Fragestellungen – in diesem Workshop anhand von
schachbasierten Rätseln, die Schülerinnen und Schüler sowie die breite
Öffentlichkeit direkt ansprechen – möchten wir vertieftes
mathematisches Denken und forschendes Explorieren fördern. Darüber
hinaus soll der Workshop auch zu einem klareren Bild davon beitragen,
was Mathematiker*innen eigentlich tun und wie mathematische Forschung
konkret abläuft.
WLAN-Zugang am Workshop
Wählen Sie auf Ihrem Laptop das Netz eth-visitors aus. Sie werden dann automatisch auf die Landing-Page für die Registrierung umgeleitet. Geben Sie dort bei Request Internet Access Ihre Handy-Nummer ein, und clicken I accept the terms of use und Request access code. Den auf dem Handy erhaltenen Code tippen Sie dann auf der Landing-Page ein und clicken submit registration. Wer kein Handy (oder ein ausländisches) hat, bittet einen anderen Kursteilnehmer die Registrierung vorzunehmen. Alternativ kann die Registrierung per Email vorgenommen werden.
| Programm | |
| ab 09:00 | Begrüssungskaffee |
| 09:30 | Beginn |
| 11:00 | Kaffee mit Brain Food |
| 13:00 - 14:00 | Mittagessen im Dozentenfoyer |
| 15:00 | Kaffee |
| 16:00 | Schluss |
